Simbol za število π je predlagal Jones, leta 1706. Euler je leta 1737 Euler prevzel Jonesov zapis števila in kmalu je postal standarden.   

Ker je π transcendentsko število zanj ne obstajajo lepi sklenjeni izrazi. Zaradi tega je treba pri računanju vzeti njegove približke, na primer dovolj: vrednost 3,14 oz. neregularni ulomek 22/7 z dolžino periode 6: 333/106.

Sumerci (okoli leta 2000 pr. n. št.) niso našli boljšega približka za π, kot je tudi poznejši biblijski π = 3, pri čemer naj bi bila ploščina kroga enaka 1/12 kvadrata njegovega obsega.   

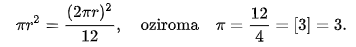
Staroegipčanski pisar Ahmes je okoli leta 1650 pr. n. št. zapisal najstarejše znano besedilo, ki podaja približno vrednost za π, ki opisuje vrednost približka 256/81 ali 3,160. V njem piše, da je ploščina kroga enaka ploščini kvadrata s stranico 8/9 premera tega kroga:   

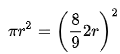
Tudi v Stari zavezi je na podlagi besedila mogoče razbrati vrednost za π, ki znaša okroglih 3.

Indijski džainistični matematiki so okoli leta 500 pr. n. št. v svojih svetih knjigah uporabljali vrednost za π s pripadajočimi začetnimi približki neskončnega verižnega ulomka:  

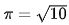
Starogrški matematiki so okrog leta 310 pr. n. št. uporabljali znani prvi približek 22/7.   

Arhimedova metoda računanja števila π: 

• Arhimed je okoli leta 230 pr. n. št. v svojem delu Merjenje kroga našel približek za obseg kroga z včrtanimi in očrtanimi pravilnimi mnogokotniki s 6, 12, 24, 48 in 96 stranicami. Ko je razširil aproksimacijo na mnogokotnike s številom stranic n = 96, je odkril:   

• 𝜋 = 3,14185110664  

Heron (okoli 20–okoli 100) je uporabljal vrednost 3.1738.

Ptolemej je okoli leta 150 izračunal vrednost v šestdesetiškem številskem sistemu in dobil 3, 1416̅.  Uporabljal je tudi vrednost π = 22/7 in 355/113.

Ču Čungdži leta 470 našel vrednost tretjega približka z navadnim končnim verižnim ulomkom 3, 14159292035398230 . Okoli leta 480 je prvo vrednost še točneje omejil z 3,14159265.